Üye Girişi
Bağlan Google+ ile Bağlan Facebook ile Bağlan
Yeni Kayıt
Tüm Forumlar
  • Tüm Forumlar
  • Eğitim ve Sınavlar
  • TYT / AYT / YDT
  • Bu Konuda
Şimdi Ara

Fizikten bir soru.

Sıcak Fırsatlarda Tıklananlar
Editörün Seçtiği Fırsatlar
Daha Fazla
Bu Konudaki Kullanıcılar: Daha Az
2 Misafir - 2 Masaüstü
5 sn
19
Cevap
1
Favori
3.202
Tıklama
Daha Fazla
İstatistik
  • Konu İstatistikleri Yükleniyor
Konuya Özel
0 oy
Öne Çıkar
Cevapla
Sayfa: 1
Giriş
Mesaj
  • Beyler şimdi
    x=v.t v=a.t ozaman x=at^2 olması gerek değilmi başındaki 1/2 nerden geliyo.



    • Yapay Zekanın Yanıtı

    Hareket Denklemleri: x = v.t ve x = 1/2at²

    Fizikte, hareket denklemleri, bir nesnenin hareketini zamana bağlı olarak tanımlayan matematiksel ifadelerdir. İki temel hareket denklemi şunlardır:

    1. x = v.t: Bu denklem, sabit bir hızla hareket eden bir nesnenin aldığı yolu (x) hızının (v) ve hareket süresinin (t) çarpımına eşit olduğunu belirtir. Birimleri sırasıyla metre (m), metre/saniye (m/s) ve saniyedir (s).

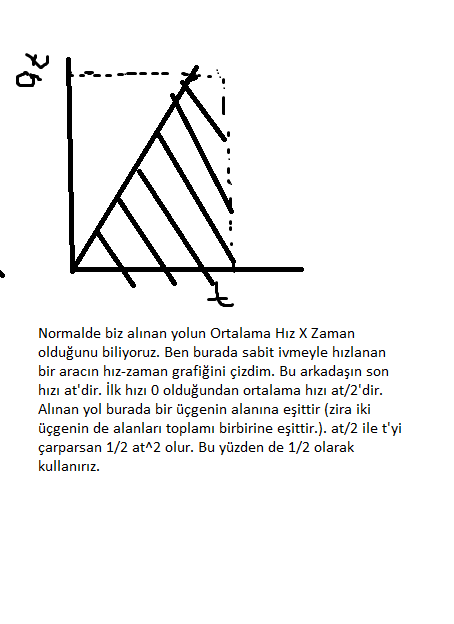
    2. x = 1/2at²: Bu denklem, sabit bir ivmeyle (a) hareket eden bir nesnenin aldığı yolu, ivmesinin, hareket süresinin karesine ve 1/2 katsayısına eşit olduğunu belirtir. Birimleri sırasıyla metre (m), metre/saniye² (m/s²), saniye (s) ve 1/2'dir.

    İlişki ve Türev

    x = v.t ve x = 1/2at² denklemleri, birbirleriyle ilişkilidir. x = v.t denklemi, x = 1/2at² denkleminin v = a.t ifadesi için türevidir. Bu, sabit bir ivmenin, sabit bir hıza neden olduğunu gösterir.

    Uygulamalar

    Hareket denklemleri, günlük hayatta çeşitli olayları anlamak ve tahmin etmek için kullanılır. Örneğin:

    • Bir aracın bir mesafeyi ne kadar sürede alacağını hesaplamak için x = v.t denklemi kullanılabilir.
    • Bir serbest düşen cismin yere çarpmadan önce ne kadar yüksekten düştüğünü hesaplamak için x = 1/2at² denklemi kullanılabilir.

    Bu denklemler, fizikteki hareket konusunun temelini oluşturur ve çok çeşitli durumlarda kullanılır.

    Yapay Zekanın Yanıtını Genişlet
  • X=v.t sabit hizli hareket icindir.İvmeli hareket oldugu icin degisiyor formul.

    < Bu ileti mobil sürüm kullanılarak atıldı >
  • quote:

    Orijinalden alıntı: HeraklesTr

    Beyler şimdi
    x=v.t v=a.t ozaman x=at^2 olması gerek değilmi başındaki 1/2 nerden geliyo.

    bak senin düşündüğün olay türevsiz basit birşey.

    x = vt formülü ivmesiz hareket için yazılmıştır. Formüllerde ortalama kavranlar kullanılmıştır mesela ortalama hız.


    Şunu o zaman şöyle düşünelim v = a*t olsun t=0 anında hızı ne bunun kardeşim ?
    Tabi ki t = 0 v = 0 olacaktır.

    t = t anında yani herhangi bir zamandaki hızı ise at dir.


    Maksimum hızı at yani peki ortalama hızı ne ?

    at/2 dir. Tabi bu doğrusal bir artış içinde olan birşeyçin geçer.

    Bunun dışındaki şeyler için türev ve integral kullanılır.


    x = vt denmez.

    dx = v(t) *dt denir.

    Çünkü v eğer ivmeli hareket yapıyorsa sabit değildir.

    Şöyle söyleyeyim v=a*t diyorsun yahu kardeşim araç 5 saniye gidiyor 1. saniyedeki hızı v1 = a*1 2. saniyedeki hız v2 = a*2 falan sen hangi hızı alacaksın sonsuz tane hız var. O yüzden hani x =v*t denilmiyor. Ya ortalaması alınır alınacak ise ya da direk üstte yazdığım gibi güzelce gösterilir.

    Türev/İntegral bilmen gerekli daha iyi kavrayabilmen için.




  • quote:

    Orijinalden alıntı: Spyxxx

    quote:

    Orijinalden alıntı: HeraklesTr

    Beyler şimdi
    x=v.t v=a.t ozaman x=at^2 olması gerek değilmi başındaki 1/2 nerden geliyo.

    bak senin düşündüğün olay türevsiz basit birşey.

    x = vt formülü ivmesiz hareket için yazılmıştır. Formüllerde ortalama kavranlar kullanılmıştır mesela ortalama hız.


    Şunu o zaman şöyle düşünelim v = a*t olsun t=0 anında hızı ne bunun kardeşim ?
    Tabi ki t = 0 v = 0 olacaktır.

    t = t anında yani herhangi bir zamandaki hızı ise at dir.


    Maksimum hızı at yani peki ortalama hızı ne ?

    at/2 dir. Tabi bu doğrusal bir artış içinde olan birşeyçin geçer.

    Bunun dışındaki şeyler için türev ve integral kullanılır.


    x = vt denmez.

    dx = v(t) *dt denir.

    Çünkü v eğer ivmeli hareket yapıyorsa sabit değildir.

    Şöyle söyleyeyim v=a*t diyorsun yahu kardeşim araç 5 saniye gidiyor 1. saniyedeki hızı v1 = a*1 2. saniyedeki hız v2 = a*2 falan sen hangi hızı alacaksın sonsuz tane hız var. O yüzden hani x =v*t denilmiyor. Ya ortalaması alınır alınacak ise ya da direk üstte yazdığım gibi güzelce gösterilir.

    Türev/İntegral bilmen gerekli daha iyi kavrayabilmen için.

    Teşekkürler 12 ye yeni geçtim bilmiyorum türev integral :D Ama anlatmak istediğini biraz anladım gibi.




  • quote:

    Orijinalden alıntı: HeraklesTr

    Teşekkürler 12 ye yeni geçtim bilmiyorum türev integral :D Ama anlatmak istediğini biraz anladım gibi.

    Şöyle söyleyeyim. Grafiğe bakarak incele;
    Fizikten bir soru.


    Şimdi x = v*t değil mi?

    v = x/t dir o zaman fakat ortalama olarak hesap yapman lazım değil mi ?

    Çünkü v dediğimiz şey her an değişiyor anlık hızı bulmamız için birazcık ileri gideceğiz şimdi.
    Analitik geometri gördüğünü farz ederek gideceğim.

    Şimdi üçgen (delta) delta x / delta t olayı var ortalama hız için fakat maalesef bunu kullanamayacağım. Çünkü yazması uzun senin için delta yerine d diyeyim. d'ler deltaların yerini tutsun (placeholder)


    şimdi v = dx/dt oldu. Güzel sade bir denklem.


    v = (Xson - Xilk)/(tson - tilk) diyeyim.

    Grafikte gördüğün üzere bak de ki 2 tane nokta belirlemişim x (yol) fonksiyonu üzerinde

    ilk nokta herhangi bir t anı olsun.
    2. nokta t+dt zamanı olur değil mi?

    t anında yolumuz x imiş olsun
    t+dt anında ise x+dx olur grafikten görebileceğin üzere.

    x(t) = (1/2)*a*t^2 fonksiyonumuz belirtildiği üzere gösteriliyor. ( a bir sabit olmak üzere )

    Şimdi

    Xson = x+dx idi
    Xilk = x idi.

    Xson -Xilk = x+dx -x = dx olacaktır.

    tson = t+dt
    tilk = t

    tson - tilk = t+dt -t = dt olacaktır.

    yani üstteki şeyi birkez daha görmüş olduk.

    v = dx/dt oluyor. (Bu biraz işlem kalabalığı oldu ama gördük yani ne diyeyim.)

    Sonracığıma asıl işe gelelim.
    Bu üstteki dx kısmını bulmamız lazım fakat dt cinsinden çünkü elimizde v = dx/dt gibi birşey var pay ile payda aynı cinsten değil ee bölemeyecez kalacak böyle armut gibi.

    O yüzden

    x(t) fonksiyonunu gösterelim.

    Xilk için t yerine t koyalım yani (1/2)*a*t^2 yi elde edelim.

    Xson için t yerine (t+dt) koyalım ve (1/2)*a*(t+dt)^2 elde edelim.

    Xson-Xilk lazım bize (1/2) *a parantezine alırsak;

    dx = (1/2) *a [ (t+dt)^2 -t^2] e oldu mu sana içeride 2 kare farkı hemen açalım;

    dx = (1/2)*a*(t+dt-t)*(t+dt+t) = (1/2)*a*dt*(2t+dt) olacaktır.

    Sonracığıma geliyor ve diyoruz ki;

    dx/dt lazım e bölelim o zaman böldüğümüzde dt ler birbirini götürecek;

    v = (1/2)*a*(2t+dt) kalacaktır.

    Şimdi işin can alıcı noktasına geldik;

    Bizim bu işlemi yapmamız için ortalama hesabı yaparken doğrusal artması lazım idi o fonksiyonun yoksa ortalama tam tutmaz.
    O yüzden diyoruz ki ah keşke doğru olsaydı 2 nokta arasından geçen çizgi.
    Aralarındaki dt mesafesini azaltırsak doğruya daha yakın olacağını fark ediyoruz.
    Diyoruz ki analitikte bir laf vardır;
    2 nokta arasından 1 doğru geçer nokta olursa eğri olur.
    O zaman diyelim ki bu zaman aralığında sadece 2 nokta bulunsun yani seçtiğimiz 2 nokta fonksiyonda yanyana olsun yan yana ne demek?
    Bu fonksiyonu oluşturan noktalar aralıksız dizildiğinden aralarında mesafe olmasın demek yani dt mesafesi sıfır olsun demek;

    dt = 0 diyince

    v = (1/2)*a*(2t+dt) = (1/2)*a*(2t+0) = a*t olur;

    yani;

    v =a*t çıkar ortaya ki

    eğer baştaki katsayı (1/2) olmasaydı 2at çıkardı ki bu yanlış olurdu;

    Bu işlemi tersten yaparak (1/2) katsayısı bulunabilir.
    Ha bir de şöyle düşün

    x = (1/2)*a*t^2 idi

    t nin üstünü çarpan olarak aldık ve üstünü bir azalttık

    v = (1/2)*2*a*t^(2-1) = a*t oldu eğer ki bir daha bu işlemi yaparsak (t^1 ya o yüzden üstünden 1 çıkarıp çarpan olarak atacaz)

    v' = a*1*t^(1-1) = a*t^0 = a olur yani bu işlemi tekrar yaparsak ivmeye ulaşırız.

    Aynı olayı

    Hacim = (4/3)*pi*r^3 formülünde r için yaparsak

    Alan = 4*pi*r^2 olan kürenin alanı ve hacmi arasındaki ilişkiyi görebilirsin.




  • quote:

    Orijinalden alıntı: Spyxxx

    quote:

    Orijinalden alıntı: HeraklesTr

    Teşekkürler 12 ye yeni geçtim bilmiyorum türev integral :D Ama anlatmak istediğini biraz anladım gibi.

    Şöyle söyleyeyim. Grafiğe bakarak incele;
    Fizikten bir soru.


    Şimdi x = v*t değil mi?

    v = x/t dir o zaman fakat ortalama olarak hesap yapman lazım değil mi ?

    Çünkü v dediğimiz şey her an değişiyor anlık hızı bulmamız için birazcık ileri gideceğiz şimdi.
    Analitik geometri gördüğünü farz ederek gideceğim.

    Şimdi üçgen (delta) delta x / delta t olayı var ortalama hız için fakat maalesef bunu kullanamayacağım. Çünkü yazması uzun senin için delta yerine d diyeyim. d'ler deltaların yerini tutsun (placeholder)


    şimdi v = dx/dt oldu. Güzel sade bir denklem.


    v = (Xson - Xilk)/(tson - tilk) diyeyim.

    Grafikte gördüğün üzere bak de ki 2 tane nokta belirlemişim x (yol) fonksiyonu üzerinde

    ilk nokta herhangi bir t anı olsun.
    2. nokta t+dt zamanı olur değil mi?

    t anında yolumuz x imiş olsun
    t+dt anında ise x+dx olur grafikten görebileceğin üzere.

    x(t) = (1/2)*a*t^2 fonksiyonumuz belirtildiği üzere gösteriliyor. ( a bir sabit olmak üzere )

    Şimdi

    Xson = x+dx idi
    Xilk = x idi.

    Xson -Xilk = x+dx -x = dx olacaktır.

    tson = t+dt
    tilk = t

    tson - tilk = t+dt -t = dt olacaktır.

    yani üstteki şeyi birkez daha görmüş olduk.

    v = dx/dt oluyor. (Bu biraz işlem kalabalığı oldu ama gördük yani ne diyeyim.)

    Sonracığıma asıl işe gelelim.
    Bu üstteki dx kısmını bulmamız lazım fakat dt cinsinden çünkü elimizde v = dx/dt gibi birşey var pay ile payda aynı cinsten değil ee bölemeyecez kalacak böyle armut gibi.

    O yüzden

    x(t) fonksiyonunu gösterelim.

    Xilk için t yerine t koyalım yani (1/2)*a*t^2 yi elde edelim.

    Xson için t yerine (t+dt) koyalım ve (1/2)*a*(t+dt)^2 elde edelim.

    Xson-Xilk lazım bize (1/2) *a parantezine alırsak;

    dx = (1/2) *a [ (t+dt)^2 -t^2] e oldu mu sana içeride 2 kare farkı hemen açalım;

    dx = (1/2)*a*(t+dt-t)*(t+dt+t) = (1/2)*a*dt*(2t+dt) olacaktır.

    Sonracığıma geliyor ve diyoruz ki;

    dx/dt lazım e bölelim o zaman böldüğümüzde dt ler birbirini götürecek;

    v = (1/2)*a*(2t+dt) kalacaktır.

    Şimdi işin can alıcı noktasına geldik;

    Bizim bu işlemi yapmamız için ortalama hesabı yaparken doğrusal artması lazım idi o fonksiyonun yoksa ortalama tam tutmaz.
    O yüzden diyoruz ki ah keşke doğru olsaydı 2 nokta arasından geçen çizgi.
    Aralarındaki dt mesafesini azaltırsak doğruya daha yakın olacağını fark ediyoruz.
    Diyoruz ki analitikte bir laf vardır;
    2 nokta arasından 1 doğru geçer nokta olursa eğri olur.
    O zaman diyelim ki bu zaman aralığında sadece 2 nokta bulunsun yani seçtiğimiz 2 nokta fonksiyonda yanyana olsun yan yana ne demek?
    Bu fonksiyonu oluşturan noktalar aralıksız dizildiğinden aralarında mesafe olmasın demek yani dt mesafesi sıfır olsun demek;

    dt = 0 diyince

    v = (1/2)*a*(2t+dt) = (1/2)*a*(2t+0) = a*t olur;

    yani;

    v =a*t çıkar ortaya ki

    eğer baştaki katsayı (1/2) olmasaydı 2at çıkardı ki bu yanlış olurdu;

    Bu işlemi tersten yaparak (1/2) katsayısı bulunabilir.
    Ha bir de şöyle düşün

    x = (1/2)*a*t^2 idi

    t nin üstünü çarpan olarak aldık ve üstünü bir azalttık

    v = (1/2)*2*a*t^(2-1) = a*t oldu eğer ki bir daha bu işlemi yaparsak (t^1 ya o yüzden üstünden 1 çıkarıp çarpan olarak atacaz)

    v' = a*1*t^(1-1) = a*t^0 = a olur yani bu işlemi tekrar yaparsak ivmeye ulaşırız.

    Aynı olayı

    Hacim = (4/3)*pi*r^3 formülünde r için yaparsak

    Alan = 4*pi*r^2 olan kürenin alanı ve hacmi arasındaki ilişkiyi görebilirsin.


    Çok saol kardeşim tam kafama yatı şimdi. Ama O zaman diyelim ki bu zaman aralığında sadece 2 nokta bulunsun yani seçtiğimiz 2 nokta fonksiyonda yanyana olsun yan yana ne demek?
    Bu fonksiyonu oluşturan noktalar aralıksız dizildiğinden aralarında mesafe olmasın demek yani dt mesafesi sıfır olsun demek;     kısmında sonraki nokta ile de arasında 0 uzaklık olur ondan sonraki ilede toplam uzunluk sıfır olmaz mı? Birde son kısım da ki işlemler hangi konu içine giriyor ?




  • quote:

    Orijinalden alıntı: HeraklesTr
    Çok saol kardeşim tam kafama yatı şimdi. Ama O zaman diyelim ki bu zaman aralığında sadece 2 nokta bulunsun yani seçtiğimiz 2 nokta fonksiyonda yanyana olsun yan yana ne demek?
    Bu fonksiyonu oluşturan noktalar aralıksız dizildiğinden aralarında mesafe olmasın demek yani dt mesafesi sıfır olsun demek;     kısmında sonraki nokta ile de arasında 0 uzaklık olur ondan sonraki ilede toplam uzunluk sıfır olmaz mı? Birde son kısım da ki işlemler hangi konu içine giriyor ?

    İki nokta arasındaki mesafe sıfır toplam mesafe tabi ki sıfırdan farklı ne demek istediğini anlayamadım diyebilirim.
    Ondan sonraki nokta ile de aradaki uzaklık sıfır mı diyorsun biraz daha açarsan daha iyi anlatabilirim.

    Son yaptığım işlemlerden kastın üstü başa indirip çarpmak ise türev kuralları konusuna girer ve bu anlattıklarım ile kuralların hepsini kanıtlayabilirsin.
    Tabi ortak çarpana alıp hepsinde paydadaki dt kısmını sadeleştirmen gerekli. Bu şekilde anlatınca çok dost canlısı bir konu gibi duruyor bence böyle anlatırım her zaman ilk defa gören arkadaşlara. Çünkü adamlar lap diye dx/dt veya dy/dx olarak görüyorlar abov diyip kalıyorlar aslında hepsi bundan ibaret türevin azıcık gökten inmiş gibi anlatılıyor o kadar.

    Ha birde kafama yattı demişsin. Eğer bu anlattıklarımı iyice anlayıp kafana oturtabildiysen ve bundan zevk (öğrenmenin verdiği haz) aldıysan kesinlikle mühendislik oku.




    • Yapay Zeka’dan İlgili Konular
    Bir parabol sorusu
    5 yıl önce açıldı
    mat1 sorusu çözemedim :( ( Zaman Denemesi)
    16 yıl önce açıldı
    bi matematik sorusu
    17 yıl önce açıldı
    Daha Fazla Göster
  • Düzgün hızlanan grafigi ciz yolu bul cevabı goreceksin

    < Bu ileti tablet sürüm kullanılarak atıldı >
  • quote:

    Orijinalden alıntı: Spyxxx

    quote:

    Orijinalden alıntı: HeraklesTr
    Çok saol kardeşim tam kafama yatı şimdi. Ama O zaman diyelim ki bu zaman aralığında sadece 2 nokta bulunsun yani seçtiğimiz 2 nokta fonksiyonda yanyana olsun yan yana ne demek?
    Bu fonksiyonu oluşturan noktalar aralıksız dizildiğinden aralarında mesafe olmasın demek yani dt mesafesi sıfır olsun demek;     kısmında sonraki nokta ile de arasında 0 uzaklık olur ondan sonraki ilede toplam uzunluk sıfır olmaz mı? Birde son kısım da ki işlemler hangi konu içine giriyor ?

    İki nokta arasındaki mesafe sıfır toplam mesafe tabi ki sıfırdan farklı ne demek istediğini anlayamadım diyebilirim.
    Ondan sonraki nokta ile de aradaki uzaklık sıfır mı diyorsun biraz daha açarsan daha iyi anlatabilirim.

    Son yaptığım işlemlerden kastın üstü başa indirip çarpmak ise türev kuralları konusuna girer ve bu anlattıklarım ile kuralların hepsini kanıtlayabilirsin.
    Tabi ortak çarpana alıp hepsinde paydadaki dt kısmını sadeleştirmen gerekli. Bu şekilde anlatınca çok dost canlısı bir konu gibi duruyor bence böyle anlatırım her zaman ilk defa gören arkadaşlara. Çünkü adamlar lap diye dx/dt veya dy/dx olarak görüyorlar abov diyip kalıyorlar aslında hepsi bundan ibaret türevin azıcık gökten inmiş gibi anlatılıyor o kadar.

    Ha birde kafama yattı demişsin. Eğer bu anlattıklarımı iyice anlayıp kafana oturtabildiysen ve bundan zevk (öğrenmenin verdiği haz) aldıysan kesinlikle mühendislik oku.



    Bunları okurken içimden ''ne zevkli konuymuş'' falan diye geçirdim :D Zaten mühendislik istiyorum bende.




  • quote:

    Orijinalden alıntı: Spyxxx

    quote:

    Orijinalden alıntı: HeraklesTr
    Çok saol kardeşim tam kafama yatı şimdi. Ama O zaman diyelim ki bu zaman aralığında sadece 2 nokta bulunsun yani seçtiğimiz 2 nokta fonksiyonda yanyana olsun yan yana ne demek?
    Bu fonksiyonu oluşturan noktalar aralıksız dizildiğinden aralarında mesafe olmasın demek yani dt mesafesi sıfır olsun demek;     kısmında sonraki nokta ile de arasında 0 uzaklık olur ondan sonraki ilede toplam uzunluk sıfır olmaz mı? Birde son kısım da ki işlemler hangi konu içine giriyor ?

    İki nokta arasındaki mesafe sıfır toplam mesafe tabi ki sıfırdan farklı ne demek istediğini anlayamadım diyebilirim.
    Ondan sonraki nokta ile de aradaki uzaklık sıfır mı diyorsun biraz daha açarsan daha iyi anlatabilirim.

    Son yaptığım işlemlerden kastın üstü başa indirip çarpmak ise türev kuralları konusuna girer ve bu anlattıklarım ile kuralların hepsini kanıtlayabilirsin.
    Tabi ortak çarpana alıp hepsinde paydadaki dt kısmını sadeleştirmen gerekli. Bu şekilde anlatınca çok dost canlısı bir konu gibi duruyor bence böyle anlatırım her zaman ilk defa gören arkadaşlara. Çünkü adamlar lap diye dx/dt veya dy/dx olarak görüyorlar abov diyip kalıyorlar aslında hepsi bundan ibaret türevin azıcık gökten inmiş gibi anlatılıyor o kadar.

    Ha birde kafama yattı demişsin. Eğer bu anlattıklarımı iyice anlayıp kafana oturtabildiysen ve bundan zevk (öğrenmenin verdiği haz) aldıysan kesinlikle mühendislik oku.



    http://img855.imageshack.us/img855/7414/adszlty.png
    Demek istediğim buydu.




  • quote:

    Orijinalden alıntı: HeraklesTr
    http://img855.imageshack.us/img855/7414/adszlty.png
    Demek istediğim buydu.

    Şimdi her bir noktanın arasındaki mesafe diyorsun ki sıfır buradaki toplam mesafe o zaman sıfır olur diye.

    Şimdi toplam mesafe = (nokta sayısı-1) * (noktalar arası mesafe)

    (Örneğin 2 nokta olsaydı arada tek mesafe olacağı için (2-1)*dt der idim.)

    Peki burada kaç tane nokta var ? Ben söyleyeyim sonsuz tane nokta var

    (sonsuz-1)*0 ediyor ki sonsuz çok büyük bir sayı olduğundan sonsuz -1 de çok büyük bir sayıdır o yüzden sonsuz'un yanında -1 ihmal edilebilir.

    sonsuz*0 = ???? şeklinde birşey karşımıza çıkar burada bunun adı belirsizliktir.

    Çünkü şöyle eğer k gibi normal bir sayıyı sonsuz ile çarpar isen cevap sonsuz olur diye bir kuralımız var. (negatif sayıları kenara koyalım)
    Sonracığıma yine k gibi bir sayıyı 0 ile çarparsan cevap sıfır olur diye de bir kuralımız var.

    Peki sonsuz*0 da hangi kural işleyecek?
    Bunu bilmiyoruz böyle bilmediğimiz durumlara belirsizlik adını veriyoruz.
    Peki bu işi nasıl çözeriz der isen şimdi 2 tane çarpanı da fonksiyon şeklinde yazarız daha sonra sadeleştirmeleri yaparız en son kalan değere bakarız.
    Çünkü kimin bu fonksiyon savaşından galip ayrıldığını baskın geldiğini görmek isteriz.

    Şöyle diyelim;

    1/10 = 0.1
    1/100 = 0.01
    1/1000 = 0.001 böyle derekn

    1/sonsuz = 0 olur denilebilir.

    Aynı şekilde

    1/0 için baktığında da değerler durmaksızın büyüyecek ve

    1/0 = sonsuz yazabileceğiz.

    Fakat bunlar yine fonksiyon tipi kavramlar yani burada limit olarak inceliyoruz 1/0 kesinlikle sonsuz diyemeyiz 1/0 = sonsuz yazmam hatadır. Çünkü tanımsızdır. Çünkü sonsuz diye bir eleman reel sayılar kümesinde tanımlı değildir. Fakat payda sıfıra yaklaşırken (yani limit adı verilen işlem) bu 1/payda nın cevabı sonsuzdur diyebiliriz.

    Bu yüzden sonsuz *0 işlemini

    sonsuz = 1/0 idi zaten diyerek

    (1/0)*0 = 0/0 veya

    0 = 1/sonsuz diyerekten

    sonsuz/sonsuz yazabiliriz.

    neyse bu temel bilgilerimizi verdikten sonra işimize dönelim.


    Herhangi 2 tane t noktası seçtik aralarındaki mesafe 10 saniye olsun (yada 10 birim)

    bu güzelim fonksiyon 10 saniyelik aralıkta n tane noktadan oluşsun.

    Her bir parçanın uzunluğu 10/(n-1) dir.

    Nokta sayısı n tane dir

    Toplam uzunluk (n-1) * 10/(n-1) dir.

    gerçek değerleri n =sonsuz olayını yani yerine yazdığında hiç fonksiyonları yadırgamadan;
    (sonsuz-1)*10/(sonsuz-1) olduğunu görecek;

    ve -1 leri ihmal edip;

    10*sonsuz/sonsuz olduğunu göreceksin;

    10*belirsizlik yani ya da şöyle dersin 10*sonsuz da çok büyük sayıdır bu da sonsuzdur o zaman

    sonsuz/sonsuz yani yine belirsizlik veya 10/sonsuz da 10*(1/sonsuz) = 10*0 = 0 diyip

    sonsuz*0 da diyebilirsin.
    Fakat üstteki (n-1)*10/(n-1) i yaptığın surette dediğimiz olay yani fonksiyonların sadeleşmesi olacak ve birbirini her zaman götürecektir.
    Çünkü fonksiyonların güçleri birbirine eşit;
    Fakat fonksiyonun uzunluğu mesela nokta sayısının karesiyle orantılı artsaydı bu söylenemeyebilirdi.

    Demem o ki aralığımızı her zaman sonsuz parçaya böleriz ve her parçanın uzunluğunun sıfır olduğunu görürüz daha sonra ise sonsuz sayıda parça ile çarparak toplam uzunluğu buluruz.


    Aynı şey şuralarda da geçerli mesela bazen adam diyor;

    a = b
    ab = b^2
    ab - a^2 = b^2 -a^2
    a*(b-a) = (b-a)*(b+a)

    (b-a)/(b-a) = (b+a)/a Burada fark edildiği üzere 1=2 imiş gibi gözükse de biz öyle demiyoruz; b-a = 0 olduğundan

    0/0 = (b+a)/a dır yani 0/0 belirsizliğinin değeri eğer her 2 fonksiyon da aynı derecede artıyorsa sabit bir sayıya eşittir. Ya da aynı şeyi

    0*sonsuz = (b+a)/a şeklinde de gösterebiliriz.




  • Fizikten bir soru.


    Spyxxx in anlatımının yanında sönük kalacak biraz ama ben de böyle anlatayım dedim
  • Hepiniz çok saolun arkadaşlar. Spyxxx türev integral ilgimi çekti araştırmaya başladım öğrenirim kendim belki :D
  • asla formül ezberleme
    grafik çizerek çöz her zaman
    ezber bilgi hata yaptırır

    < Bu ileti mobil sürüm kullanılarak atıldı >
  • asla formül ezberleme
    grafik çizerek çöz her zaman
    ezber bilgi hata yaptırır

    < Bu ileti mobil sürüm kullanılarak atıldı >
  • quote:

    Orijinalden alıntı: ihaveaquestion

    asla formül ezberleme
    grafik çizerek çöz her zaman
    ezber bilgi hata yaptırır

    Haklısın zaten ezberlemediğimden dolayı çıktı bu olay denebilir. Soruyu çözerken x=v.t den falan gidiyodum 2 katı çıktı sonuç sonra altta çözümü görünce böylee bir formul olduğunu gördüm :D
  • hocam simdi x=v.t burdaki v ortalama hız 0 dan ivmeleniyorsa ilk hız 0 son hız a.t ort a.t/2 olur bunuda t ile carparsan yolu bulursun turev integrali unut gitsin
  • of reis ne anlatmışın üst başa geliyo işte:D
  • @MrTrM

    Bence kısa, öz ve güzel anlatmışsın kendine haksızlık etme benim de aklıma geldi bu yöntem ama sorunu kökten çözeyim dedim çünkü ileride yine benzer sorunlar yaşayacak ya elindeki grafik parabolik olursa ne yapmalı şimdi alanını bul desem bulması zor olur bulamayabilir. Fakat senin grafiğin ile de olayın pekiştiğini düşünüyorum. Hatta senin grafiğinin üzerinden giderek de anlatayım.

    _______________________________

    Fizikten bir soru.


    Az önce yaptığım hani mesafeyi n tane parçaya bölme olayının uygulamasını göstereyim.
    Şimdi diyelim ki elimizde böyle bir alan var bulacağız fakat bulamıyoruz ne yapmalıyız?
    Bu alanı dikdörtgenlerden oluşmuş kabul etmek işimize yarayabilir. Dikdörtgenlerden oluşmuş kabul edeceğiz fakat hatayı da minimuma indirmek istiyoruz ne yapmalıyız dersek dikdörtgenlerin kalınlığını (dt) sıfıra yaklaştırırsak hatamız da sıfıra yaklaşır.

    Şöyle ki (0,t) aralığını (açık aralık veya kapalı aralık olması pek önemli değil sonsuz küçük hata içerir.)
    n tane parçaya bölerim. Her bir parçanın büyüklüğü (Toplam Uzunluk)/n olduğundan dolayı t/n olmuş olur.
    Sonracığıma bu elimdeki parçanın kalınlığı değil mi? Birde dikdörtgenin uzunluğu var o da f(t) dediğimiz uzunluk yani fonksiyonumuz a*t dir. Uzunluk ve kalınlığını çarpıp tüm dikdörtgenleri toplarsak;

    Bir dikdörtgenin alanı = a*t *t/n = at^2/n oluyor.

    peki bu işlemi nereden nereye yapacağız dersek;

    Toplam sembolü 1 den n 'e kadar bu işlemi yapmalıyız;

    sonracığıma başına da limit n->sonsuza giderken eklemeliyiz.
    Bunu çözdüğümüzde yine bir belirsizlik gelecek limit tarafını kullanarak da sadeleştirmelerimiz ile soruyu çözeceğiz. Bu işleme riemann toplamları adı veriliyor. Peki diyorsan ki dikdörtgen minimum 2 noktadan oluşabilir peki hangisini alacağız diye. Alttaki noktayı alırsan alt riemann, üstteki noktayı alırsan üst riemann toplamlarını bulmuş olursun.

    Peki biz bunu bu kadar karıştırmaz da bırakırsak yani

    f(t)*dt olarak yazarsak da diferansiyel bir ifade oluyor başına sonsuz toplam gibi korkutucu bir ifade koymak yerine integral işareti koyup daha sonra başına sonuna başlangıç ve son değerlerimizi yazarsak integral işlemini tanımlamış oluruz ki güzel birşeydir bu.

    ____________

    Bu arada integral ve türev hayatın bir parçasıdır birşeyleri ezberlememek istiyorsan onları bir kenara atmadan çalışmanı ve uygulamanı tavsiye derim. Hadi konudayken bir örnek daha vermiş olalım bu sefer 2 boyutlu dairemizle ilgili bir örnek olsun;

    A = pi*r^2 bunun türevi
    U = 2*pi*r oluyor. Bu da uzunluk-alan arasındaki güzel ilişkiyi veriyor diyebilirim.




    • 
Sayfa: 1

Benzer içerikler

- x
Bildirim
mesajınız kopyalandı (ctrl+v) yapıştırmak istediğiniz yere yapıştırabilirsiniz.
Hizmet kalitesi için çerezleri kullanabiliriz, DH'yi kullanırken depoladığımız çerezlerle ilgili veri politikamıza gözatın.
Kabul Ediyorum