Yeni Kayıt
1 Mobil
Konudaki Resimler
< Bu ileti mobil sürüm kullanılarak atıldı > |
(a+b+c)³ Açılımı
İkinci dereceden üç terimli ifadenin kübü, yani (a+b+c)³, şu şekilde açılır:
$$(a+b+c)^3 = a^3 + b^3 + c^3 + 3(a^2)(b+c) + 3(b^2)(a+c) + 3(c^2)(a+b) + 6abc$$
Bu açılımda, ilk üç terim, her bir değişkenin üçüncü kuvvetidir. Kalan terimler ise ikinci dereceden ifadelerin çarpımı ile elde edilen çarpım terimleridir.
Örnek:
(a+b)² açılımı:
$$(a+b)^3 = a^3 + b^3 + 3a^2b + 3ab^2$$
Diğer Örnekler:
- (x+y+z)³ açılımı:
$$(x+y+z)^3 = x^3 + y^3 + z^3 + 3(x^2)(y+z) + 3(y^2)(x+z) + 3(z^2)(x+y) + 6xyz$$
- (x+2)³ açılımı:
$$(x+2)^3 = x^3 + 8 + 3x^2(2) + 3x(2)^2$$
İpucu:
İfadenin küpünü açmak için üçüncü dereceden bir binom açılımı uygulayabilirsin. Bu, (a+b)³ gibi daha basit ifadelerden daha karmaşık ifadelere kadar çeşitli ifadelerin küplerini açmana yardımcı olacaktır.
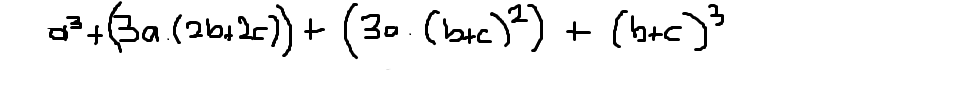
düzenle sonuç karsında 
Hızlı 
