Yeni Kayıt
1 Mobil
Konudaki Resimler
 Şu sorudaki gibi x.f(x)dx belirli integrali nasıl hesaplanıyor acaba? |
{x.f(x) integrali} Hesaplama
{x.f(x) integrali}, {f(x) integrali} ile x'in çarpımının integralleridir. Bu tür integralleri hesaplamak için çarpımın integrali kuralı kullanılır.
Çarpımın integrali kuralına göre, {x.f(x) integrali}, {f(x) integrali}nin x türevi ile {f(x) integrali}nin çarpımından çıkarılarak hesaplanır:
$$\int x.f(x) \ dx = x \int f(x) \ dx - \int \left(\frac{d}{dx}(x) \int f(x) \ dx \right) \ dx$$
Burada, (\frac{d}{dx}(x)) x'in türevidir, yani 1'dir.
Bu kuralı kullanarak {x.f(x) integrali} aşağıdaki şekilde hesaplanır:
$$\int x.f(x) \ dx = x \int f(x) \ dx - \int \left(1 \cdot \int f(x) \ dx \right) \ dx$$
$$\int x.f(x) \ dx = x \int f(x) \ dx - \left(\int f(x) \ dx \right)^2 + C$$
Burada, C, integrallemenin sabitidir.
Bu formülü kullanarak, {xf(x) integral}, {x f(x) integral} veya {fx in integrali} gibi farklı ifadelerle verilen integraller hesaplanabilir. Örneğin:
- {x.sin(x) integrali} = x (\int) sin(x) \ dx - (\left(\int) sin(x) \ dx \right)^2 + C
- {x.e^x integrali} = x (\int) e^x \ dx - (\left(\int) e^x \ dx \right)^2 + C
- {x.ln(x) integrali} = x (\int) ln(x) \ dx - (\left(\int) ln(x) \ dx \right)^2 + C
Çarpımın integrali kuralını kullanarak, {x.f(x) integrali} ve benzeri integralleri kolayca hesaplayabilirsin.
Alexander Volg Zangief
kullanıcısına yanıt
kullanıcısına yanıt
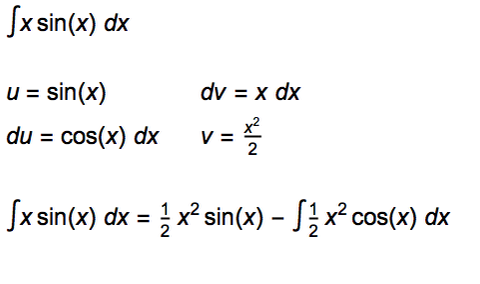
Hızlı 
