Bildirim
Gölgesinden Ağacın Boyunu Ölçmek
Bu Konudaki Kullanıcılar:
2 Misafir (1 Mobil) - 1 Masaüstü,  1 Mobil
1 Mobil
 1 Mobil
1 Mobil

Giriş
Mesaj
-
-
Pisagor Teoremi'nden yapılabilir bence, aşağıdaki resimde açıkladım 
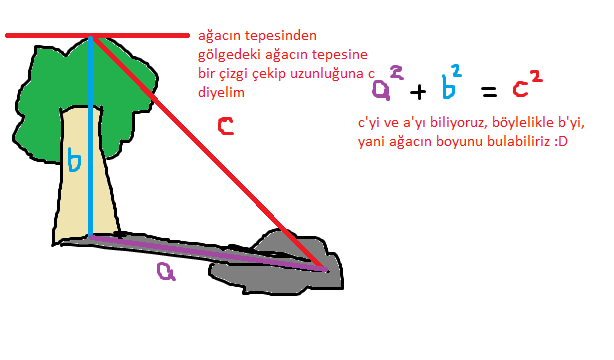
Umarım yardımcı olabilmişimdir.
-
Boyu bilinen 1-2 metrelik bir çubuk ağacın yanına ağaca paralel olarak saplanır, çubuğun boyu ile gölgesinin oranı, ağacın boyu ile gölgesinin oranı ile aynı olacaktır. Dolayısı ile ağacın gölgesinden basit bir çarpma işlemi bu oran sayesinde boyu bulunabilir.
Ya da
Ağacın gölgesinin ucundan ağacın tepesine bir ip çekilir. İpin yer ile yaptığı açı, gölge boyu ve ipin boyu kullanılarak kosinüs teoremine başvurulur.(http://tr.wikipedia.org/wiki/Kosin%C3%BCs_teoremi)
Elbette ipi çekmek ağacın boyunu ölçmekten çok çok daha zahmetli bir iş olacağı için rasyonel düşünen her insan ilk yöntemi kullanacaktır bu yüzden ikinci yöntemden bahsetmek bile saçma olur aslında
Ben bu iletiyi yazarken bir arkadaş pisagor teoreminden bahsetmiş o da verdiğim ikinci yöntemle aynı kapıya çıkıyor, gereksiz ve faydasız. Kaldı pisagor teoreminden faydalanmak için ağacın yere tam olarak dik konumda olması gerekir (Çoğu ağaç değildir.). Aksi halde sonuç hatalı olacaktır.
< Bu mesaj bu kişi tarafından değiştirildi Homo juridicus -- 29 Aralık 2012; 21:25:39 >
-
quote:
Orijinalden alıntı: kerlonmoura
Pisagor Teoremi'nden yapılabilir bence, aşağıdaki resimde açıkladım

Umarım yardımcı olabilmişimdir.
Böyle yapacağına direk ağacın altına çekersin ipi.
Ağacın ucundan gölgenin düştüğü son nokta arası açıyı hesaplarsın açıölçerle. Açının cos değeriyle uzunluğu çarparsan gölgenin ağacın boyu çıkar
-
Kardeş yeğenine sorduklarına göre, yeğenin de kapı kapı dolaştığına göre belli ki ilkokul öğrencisi kendisi sen hiç karıştırma kosinüsleri de çocuğun aklı karışmasın. En güzeli dediğim gibi:
Boyu bilinen 1-2 metrelik bir çubuk ağacın yanına ağaca paralel olarak saplanır, çubuğun boyu ile gölgesinin oranı, ağacın boyu ile gölgesinin oranı ile aynı olacaktır. Dolayısı ile ağacın gölgesinden basit bir çarpma işlemi bu oran sayesinde boyu bulunabilir. -
quote:
Orijinalden alıntı: Homo juridicus
Boyu bilinen 1-2 metrelik bir çubuk ağacın yanına ağaca paralel olarak saplanır, çubuğun boyu ile gölgesinin oranı, ağacın boyu ile gölgesinin oranı ile aynı olacaktır. Dolayısı ile ağacın gölgesinden basit bir çarpma işlemi bu oran sayesinde boyu bulunabilir.
Evet, bu çok daha mantıklı, konu sahibi bunu kullansın
< Bu mesaj bu kişi tarafından değiştirildi kerlonmoura -- 29 Aralık 2012; 21:29:11 > -
quote:
Orijinalden alıntı: Homo juridicus
Kardeş yeğenine sorduklarına göre, yeğenin de kapı kapı dolaştığına göre belli ki ilkokul öğrencisi kendisi sen hiç karıştırma kosinüsleri de çocuğun aklı karışmasın. En güzeli dediğim gibi:
Boyu bilinen 1-2 metrelik bir çubuk ağacın yanına ağaca paralel olarak saplanır, çubuğun boyu ile gölgesinin oranı, ağacın boyu ile gölgesinin oranı ile aynı olacaktır. Dolayısı ile ağacın gölgesinden basit bir çarpma işlemi bu oran sayesinde boyu bulunabilir.
Çok mantıklı bu, benim de aklıma direkt kosinüs geldiydi
-
benim aklıma şöyle bir şey geldi ama mantıklımı bilemiyorum agacın gölgesinin yanına biri durur o kişinin ve agacın gölgesi ayrı ayrı ölçülür daha sonra kişinin boyu ölçülür
örneğin kişinin gölgesi 3 metre agacın gölgesi 9 metre geldi diyelim akabinde kişinin boyu ölçülür o da diyelim ki 1.50 metre geldi bu da demektir ki 1 e 2 oranı var bu taktirde ağacın 9 metre gelen gölgesinin yarısı kadar boyu yani 4.50 cm boyu olur -
quote:
Orijinalden alıntı: kerlonmoura
quote:
Orijinalden alıntı: Homo juridicus
Boyu bilinen 1-2 metrelik bir çubuk ağacın yanına ağaca paralel olarak saplanır, çubuğun boyu ile gölgesinin oranı, ağacın boyu ile gölgesinin oranı ile aynı olacaktır. Dolayısı ile ağacın gölgesinden basit bir çarpma işlemi bu oran sayesinde boyu bulunabilir.
Evet, bu çok daha mantıklı, konu sahibi bunu kullansın
Öss mağduruyuz hepimiz benim de aklıma ilk kosinüs gelmişti aslında.
-
ilk mesajda belirtmeyi unutmuşum arkadaşlar kusura bakmayın yeğenim 7.sinifa gidiyor. cevaplariniz için çok teşekkür ediyorum. Homo juridicus arkadaşınkini kullanabiliriz. başka önerilerileri de bekliyorum.
< Bu mesaj bu kişi tarafından değiştirildi pallad -- 29 Aralık 2012; 22:08:00 >
< Bu ileti mobil sürüm kullanılarak atıldı > -
eğer güneşin geliş açısı hesaplanır ise trigonometriden rahatlıkla bulunabilir. 
edit:
@Homo juridicus arkadaşımızın dediği gibi yapılır.Başka kolay çözüm yok.
< Bu mesaj bu kişi tarafından değiştirildi Girrffe -- 30 Aralık 2012; 2:13:24 > -
total station kullan 

Sayfa:
1
Ip işlemleri
Bu mesaj IP'si ile atılan mesajları ara Bu kullanıcının son IP'si ile atılan mesajları ara Bu mesaj IP'si ile kullanıcı ara Bu kullanıcının son IP'si ile kullanıcı ara
KAPAT X
Bu mesaj IP'si ile atılan mesajları ara Bu kullanıcının son IP'si ile atılan mesajları ara Bu mesaj IP'si ile kullanıcı ara Bu kullanıcının son IP'si ile kullanıcı ara
KAPAT X






 Yeni Kayıt
Yeni Kayıt






 Konudaki Resimler
Konudaki Resimler



 Hızlı
Hızlı 



















