Bildirim
Dik üçgen sorularım
Daha Fazla 
Bu Konudaki Kullanıcılar:
Daha Az
2 Misafir (1 Mobil) - 1 Masaüstü,  1 Mobil
1 Mobil
 1 Mobil
1 Mobil

Giriş
Mesaj
-
-
up -
up -
çözecektim de uzun olacağını farkettim buradan anlatacağım hepsini.
3. soru:
AD ve BC doğrularını uzatın. 30 60 90 dolayısıyla ve 120 derece dolayısıyla eşkenar üçgen oluşacak. diğer kenarlara da 3 yazın. Hipotenüsü (x+3) olan 60'ın karşısı 8(kök3) olan bir dik üçgenimiz var. trigonometrik işlemlerden sonra: x+3=16.
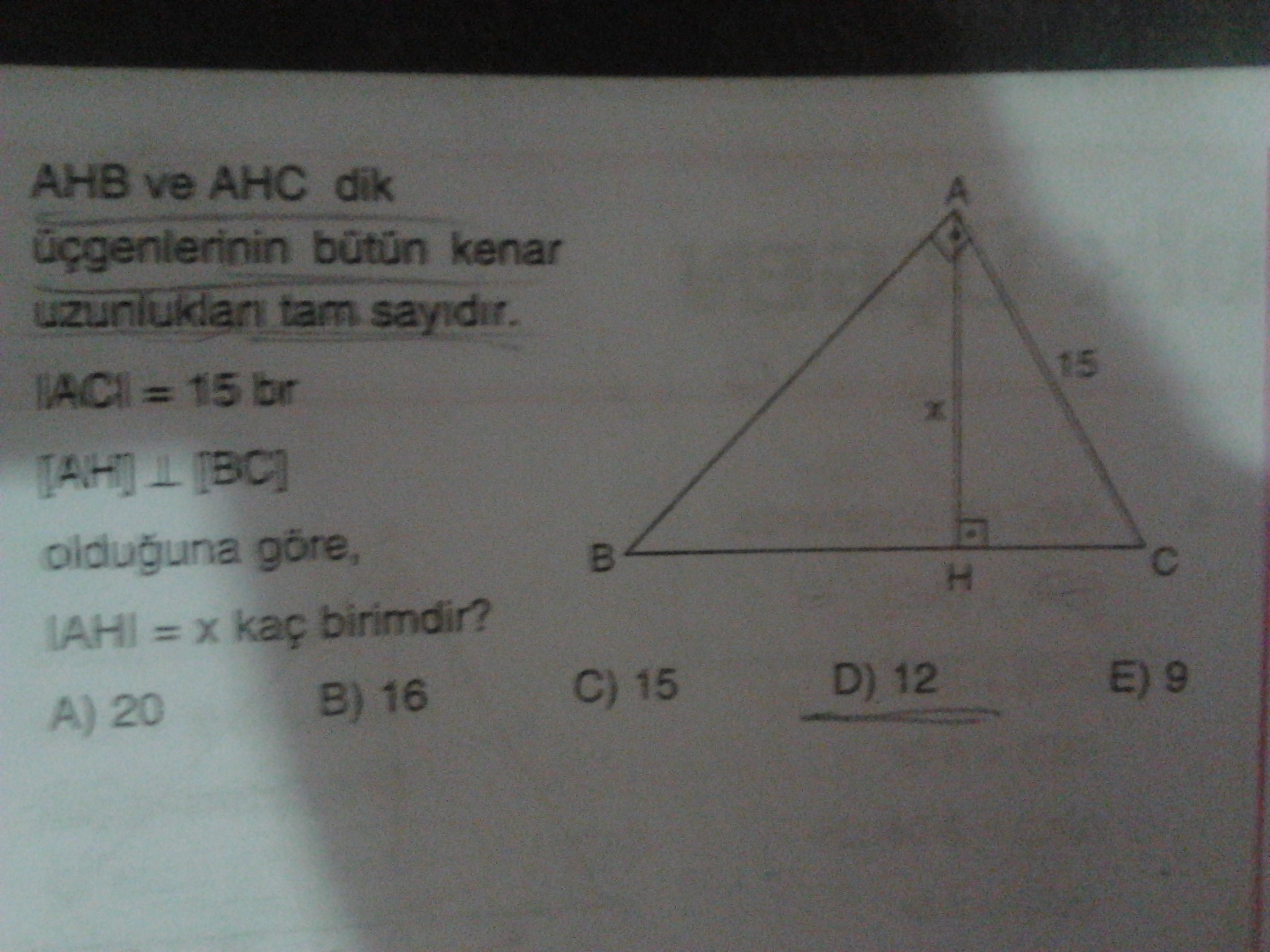
6. soru:
6. soru da öklid kuralından birbiri cinsinden bağıntıları yazmalısın. benzerlik de deneyebilirsin yine aynı bağıntılar çıkıyor. bh ve hc kenarlarına değer vermelisin sanıyorum çünkü biraz uğraşmama rağmen direkt ulaşma yolunu bulamadım.
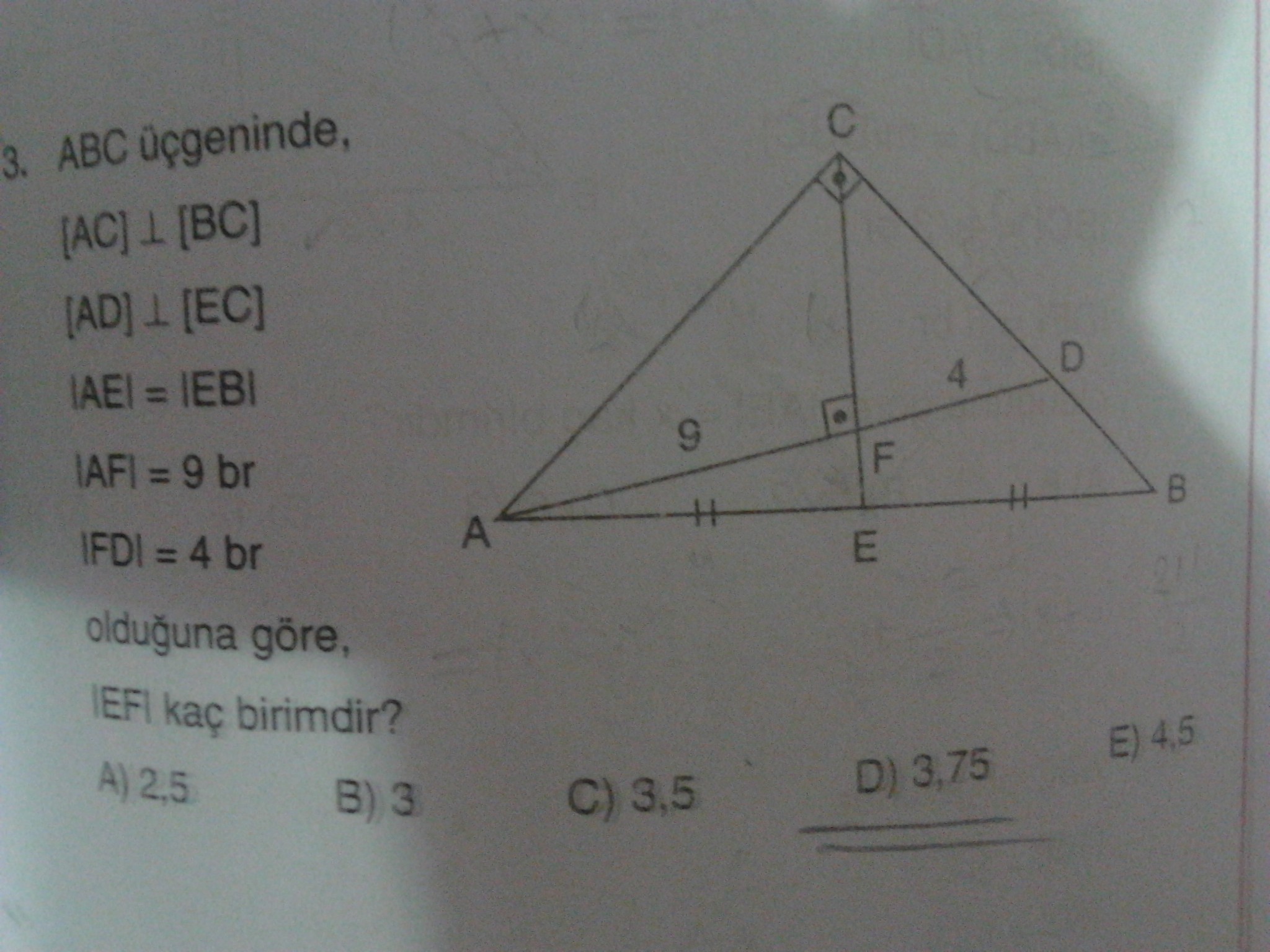
5. soru:
burada görmen gereken 2 kural var birincisi öklid bağıntısı: cf'nin 6 olduğunu gör. İkinci görmen kural ise muhteşem üçlü. ce diğer eşit olan parçalara eşit olur. fe'ye x dersek ae x+6 olur; karelerini alıp hipotenüsün karesine eşitlersen cevabı bulursun.
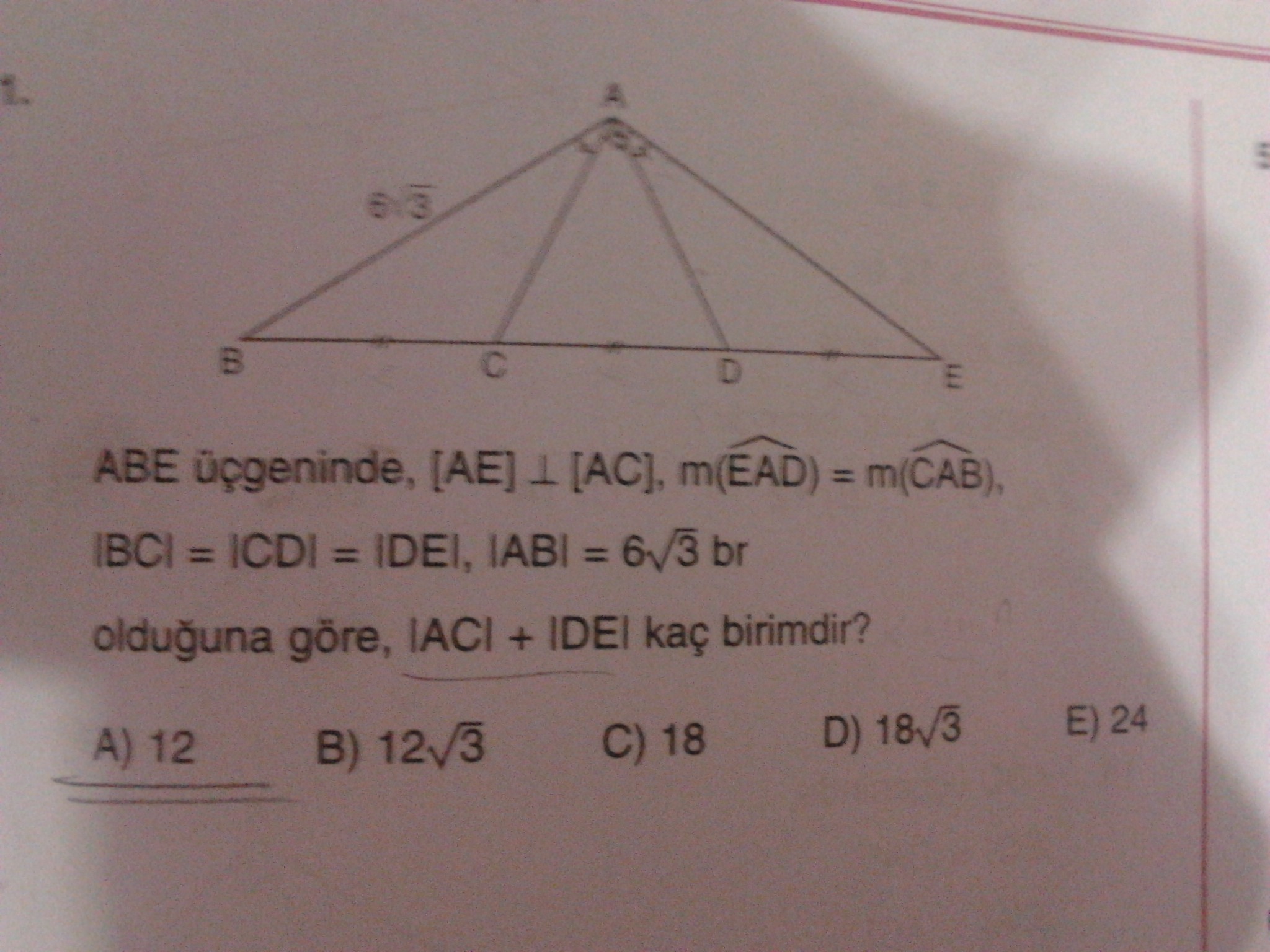
1. soru:
bu sorunun daha kolay bir yolu var mı bilmiyorum ama 15-75-90 üçgeni özelliklerinden önce BD'yi sonra diğer 15-75-90 üçgenini kullanıp BE'yi bulursun. Büyük üçgende 30-60-90'dan BC'yi bulursun. BC'den BE'yi çıkartır ve sonuca ulaşırsın.
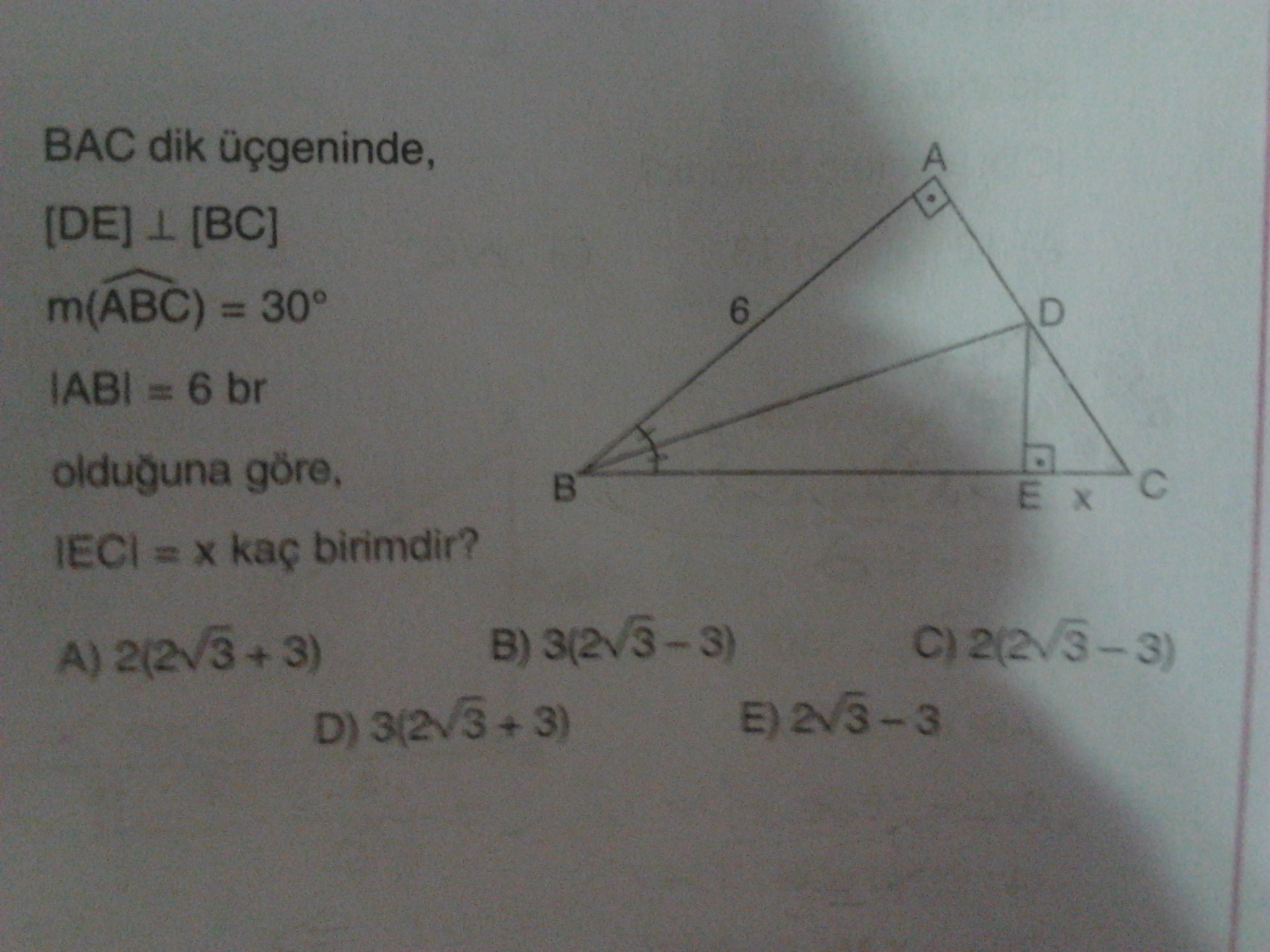
2. soru:
Eğer ACD açısına b der eşit olan açılara a dersen eğer 2 tane dik üçgen olduğunu görürsün. a+b 90 olduğundan (ac diktir ae bağıntısını kullanıyoruz) ac ve ad muhteşem üçlüden eş olan diğer üç kenara eşit eşit çıkar. ACD üçgeni eşkanr olduğundan ACB açısı 120 derecedir. 120-30-30 üçgeninden ac be BC'yi 6 buluruz. Zaten eş olduklarından 6+6'dan 12.
Bence biraz muhteşem üçlünün özelliklerine çalışmalısın.
ekleme: 4'ü yazmayı unutmuşum.
ab'yi ve ec'yi uzatırsan abc üçgenine eş üçgen oluşturursun. cb'ye m ec'ye n dersek oluşturduğumuz üçgenden dolayı, doğrusal m+n uzunluğunda bir doğrumuz olur. e noktasından ba'ya dik çekerseniz oluşan kısım bd'den dolayı 12 olacaktır. diğer kenar da diğer bağıntıdan 12 olacaktır. cevap 12(kök2)
< Bu mesaj bu kişi tarafından değiştirildi yagmur adam -- 23 Aralık 2012; 20:11:43 >
-
quote:
Orijinalden alıntı: yagmur adam
çözecektim de uzun olacağını farkettim buradan anlatacağım hepsini.
3. soru:
AD ve BC doğrularını uzatın. 30 60 90 dolayısıyla ve 120 derece dolayısıyla eşkenar üçgen oluşacak. diğer kenarlara da 3 yazın. Hipotenüsü (x+3) olan 60'ın karşısı 8(kök3) olan bir dik üçgenimiz var. trigonometrik işlemlerden sonra: x+3=16.
6. soru:
6. soru da öklid kuralından birbiri cinsinden bağıntıları yazmalısın. benzerlik de deneyebilirsin yine aynı bağıntılar çıkıyor. bh ve hc kenarlarına değer vermelisin sanıyorum çünkü biraz uğraşmama rağmen direkt ulaşma yolunu bulamadım.
5. soru:
burada görmen gereken 2 kural var birincisi öklid bağıntısı: cf'nin 6 olduğunu gör. İkinci görmen kural ise muhteşem üçlü. ce diğer eşit olan parçalara eşit olur. fe'ye x dersek ae x+6 olur; karelerini alıp hipotenüsün karesine eşitlersen cevabı bulursun.
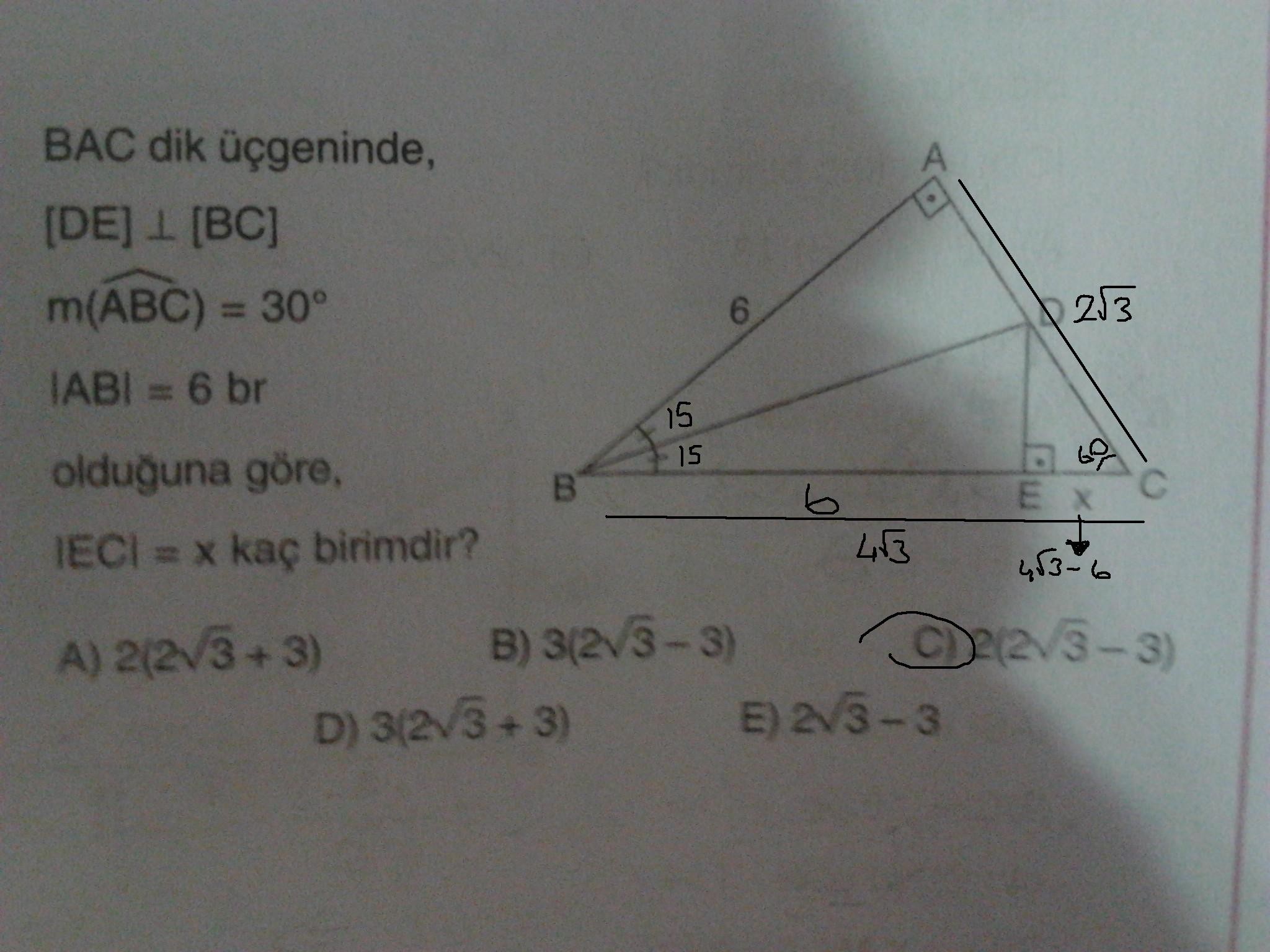
1. soru:
bu sorunun daha kolay bir yolu var mı bilmiyorum ama 15-75-90 üçgeni özelliklerinden önce BD'yi sonra diğer 15-75-90 üçgenini kullanıp BE'yi bulursun. Büyük üçgende 30-60-90'dan BC'yi bulursun. BC'den BE'yi çıkartır ve sonuca ulaşırsın.
2. soru:
Eğer ACD açısına b der eşit olan açılara a dersen eğer 2 tane dik üçgen olduğunu görürsün. a+b 90 olduğundan (ac diktir ae bağıntısını kullanıyoruz) ac ve ad muhteşem üçlüden eş olan diğer üç kenara eşit eşit çıkar. ACD üçgeni eşkanr olduğundan ACB açısı 120 derecedir. 120-30-30 üçgeninden ac be BC'yi 6 buluruz. Zaten eş olduklarından 6+6'dan 12.
Bence biraz muhteşem üçlünün özelliklerine çalışmalısın.
ekleme: 4'ü yazmayı unutmuşum.
ab'yi ve ec'yi uzatırsan abc üçgenine eş üçgen oluşturursun. cb'ye m ec'ye n dersek oluşturduğumuz üçgenden dolayı, doğrusal m+n uzunluğunda bir doğrumuz olur. e noktasından ba'ya dik çekerseniz oluşan kısım bd'den dolayı 12 olacaktır. diğer kenar da diğer bağıntıdan 12 olacaktır. cevap 12(kök2)
çok teşekkür ederim. 4.soruda en küçük değer demiş bir şey farkeder mi
-
Sayfa:
1
Ip işlemleri
Bu mesaj IP'si ile atılan mesajları ara Bu kullanıcının son IP'si ile atılan mesajları ara Bu mesaj IP'si ile kullanıcı ara Bu kullanıcının son IP'si ile kullanıcı ara
KAPAT X
Bu mesaj IP'si ile atılan mesajları ara Bu kullanıcının son IP'si ile atılan mesajları ara Bu mesaj IP'si ile kullanıcı ara Bu kullanıcının son IP'si ile kullanıcı ara
KAPAT X






 Yeni Kayıt
Yeni Kayıt






 Konudaki Resimler
Konudaki Resimler





 Hızlı
Hızlı 



















