Limit

Sorunun cevabı D'ymiş.

Ama ben şöyle düşünerek b bulmuştum.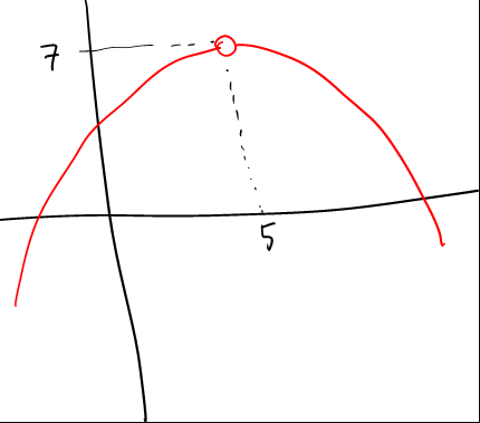

mesela fonksiyon böyle olsa, lim x=5 için f(5) = 7 çıkar ama f(5) = 7 olmaz. Süreklilik de olmaz. Dolayısıyla x=5te tanımlı da olmaz. bunun aksini de yapabileceğimiz için her zaman için istenen durumu sağlayamayız.

bu yüzden 3-4-5 yanlış olur dedim. fakat hatalıymışım. hatam nerede anlatır mısınız rica etsem?

teşekkür ederim hocam

Hocam bir arkadaş bu soruyu öğretmenlerine sormuş. O da "limx->5 f(x)'i o şekilde parçayalamazsınız, direkt f(5)-7=0 olmalı bu yüzden f(5)=7 olmalı" diye çözüm yapmış. Sorunun cevabını da 4 öncül doğru olarak değerlendiriyor. Kafam karıştı şimdi, benim çözüm neden olmuyor ki?

Aynen, biraz daha düşündüm üzerine ama bir sıkıntı bulamadım. Mesela bir örnek yapalım,

pay kısmı 4(x-5)'e eşit olursa istenen limit 4 olur,

bunun için f(x)=4x-13 olması gerek.

Şimdi f'in x=5'te tanımlılığını kaldıralım, yani f(x)'i şöyle parçalayarak yazabiliriz,

f(x) = { 4x-13, x∈R-{5};

tanımsız, x=5}.

Pay kısmına g(x) diyelim, o zaman pay kısmı

g(x) = {4x-20, x∈R-{5},

tanımsız, x=5}.

lim x->5'e giderken g(x)/(x-5) değerini bulurken hiçbir zaman x yerine 5 yazmayız, pay ve paydadaki fonksiyonların x=5'teki görüntüleriyle ilgilenmeyiz, 5'in yakınındaki değerleri yazarız.

g(x)/(x-5)=(4x-20)/(x-5)=[4*(x-5)]/(x-5).

Örneğin sağdan yaklaşalım,

x=5.1 için, (x-5)/(x-5) ifadesi = 0.1/0.1=1 olur, bu yüzden sonuç 4*1=4 oldu.

x=5.01 için de (x-5)/(x-5) = 0.01/0.01=1, sonuç 4*1=4.

x=5.001 için yine (x-5)/(x-5)=0.001/0.001=1, sonuç 4.

x=5 dışındaki tüm x sayıları için, (x-5)/(x-5) ifadesi 1'e eşit olur, sonuç 4*1=4 olur. O yüzden soldan yaklaşırken de yine aynı şekilde sonuç 4 olur. Yani x=5'te tanımlı olmaması hiçbir şeyi değiştirmedi,

g(x)/(x-5)'in grafiğini çizersek grafik yatay y=4 grafiğidir, yalnızca x=5'te boşluk vardır, 5'e giderkenki limit yine 4'e eşit.

Bu atılan soru için sadece 1. öncül doğru olmaz mı ben de öyle buldum

Aynen, daima doğru olan yalnızca 1. öncül. Diğerleri doğru olabilir de, olmayabilir de.

çok teşekkür ederim hocam