L'hospital

-
-
türev olduğu için kesinlikle süreklidir doğru
< Bu ileti Android uygulamasından atıldı > -
zaten sürekli olmazsa 2. öncül de kesinlikle doğru olmaz. biz sadece f(-2)=-2 olduğunu biliyoruz. -2'de limit değerinin de -2 olması için kesinlikle sürekli olmalı
< Bu ileti Android uygulamasından atıldı > -
Fonksiyonun ne olduğunu bilmediğimiz için l'hospital i direkt uygulayamayız. isterseniz x=-2 de süreksiz olup bu durumu sağlayan f fonksiyonu yazıp atabilirim.
< Bu ileti mobil sürüm kullanılarak atıldı > -
f(-2)=-2 olduğu kesindir. eğer 2. öncüle kesinlikle doğru diyebiliyorsak -2 noktasında süreklidir. türevi olmayabilir orda haklı olabilirsin, bu sefer de hiçbir öncül kesinlikle doğru olmaz. böyle bir fonksiyon yazabilir misin merak ettim
< Bu ileti Android uygulamasından atıldı > -
-
papazefendiye katılıyorum,ayrıca senin yazdığın fonksiyonda 2 noktası fonksiyonun tanım kümesinde olamayacağı için süreklilik inceleyemezsin. -
Adam onu diyor zaten -2 de süreksiz olup bu durumu sağlayan fonksiyon yazdı -
güzel örnek ama hala f(-2) değerinin de tanımlı olması gerektiğini düşünüyorum. kafam karıştı migma hocam bakabilir misin?
< Bu ileti Android uygulamasından atıldı > -
arkadaşım bir noktada süreklilik inceleyebilmek için o noktanın tanım kümesinde olması lazım -2 noktasını fonksiyona koyamadığın için sürekli yada değil yorumunu yapmazsın. -
-
tanımlı derken direkt f(-2)=-2 olmalı anlamında demiştim. f(-2)=99999 olursa 0/0 belirsizliği olmuyor zaten
< Bu ileti Android uygulamasından atıldı > -
Haklısın göz ardı etmişim kusura bakma -
Hocam bizim f(-2) ile işimiz yok ki biz sağdan soldan limitlerle ilgileniyoruz.
< Bu ileti mobil sürüm kullanılarak atıldı > -
bana 0/0 belirsizliği kesin olmalıymış gibi geliyor yani pay kısmının da 0 olması gerektiğini düşünüyorum ama senin yazdığın örnekte de sıkıntı yok gibi. kafamı da burası karıştırıyor
< Bu ileti Android uygulamasından atıldı > -
Hocam limit sorularında x yerine direkt sayıyı koymaya alışmışsınız. Polinom içeren sorularda doğru bir hareket ama bunun gibi sorularda biraz düşünmek lazım. Dikkat hocam sınavda başınız yanmasın.
< Bu ileti mobil sürüm kullanılarak atıldı > -
Limitini aliyorsun zaten sureklilik zorunlu değil ki
< Bu ileti mobil sürüm kullanılarak atıldı > -
Tabii hocam. 0/0 belirsizliği şu demek değil:
"limitte yaklaşılan değer için pay ve paydadaki fonksiyonlar 0'a eşit oluyorsa 0/0 belirsizliği vardır" bu değil, yani
"lim x->a [f(x)/g(x)] ifadesinde, f(a)=0 ve g(a)=0 ise 0/0 belirsizliği vardır", bu değil.
0/0 belirsizliği şu:
Yaklaşılan değer neyse, x o değere yaklaşırken pay kısmındaki fonksiyon da 0'a yaklaşıyor yani limiti 0, paydadaki fonksiyon da 0'a yaklaşıyor yani limiti 0, bu şekilde hem paydaki, hem de paydadaki fonksiyonlar ayrı ayrı 0'a yaklaşıyor ise 0/0 belirsizliği vardır. Yani:
lim x->a [f(x)/g(x)] ifadesinde, lim x->a f(x)=0 ve lim x->a g(x)=0 ise 0/0 belirsizliği vardır.
lim x->a g(x)=0 iken lim x->a [f(x)/g(x)] limiti bir reel sayıya eşitse, yani paydanın limiti 0 iken bölümün limiti bir reel sayıya eşitse, bu ancak payın limiti de sıfıra eşit ise mümkün oluyor, yani aynı zamanda
lim x->a f(x) = 0 olmalı.
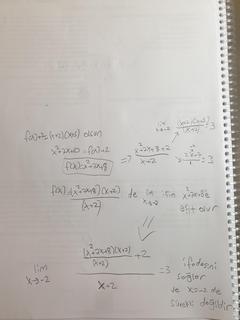
Bu soruda, paydaya g(x) diyelim yani g(x)=x+2,
g(-2)=0 olduğu için değil;
lim x->-2 g(x)=0 olduğu için 0/0 belirsizliği var, o yüzden x->-2'ye giderken payın limiti de sıfır olmak zorunda,
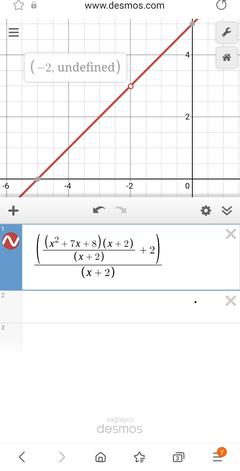
lim x->-2 [f(x)+2] = 0. Ama f(-2)+2=0 olmak zorunda değil, f(-2) tanımlı bile olmayabilir yukarıdaki arkadaşın dediği gibi. Buradan da şu gelir:
lim x->-2 f(x) = -2. Tüm bulabildiğimiz budur. f fonksiyonu x=-2'de tanımlı olmayabilir, tanımlı olup değeri -2'den farklı bir şey de olabilir.
L'hopital olayına da dikkat etmek lazım, L'hopital uygulayabilmek için belli şartların olması lazım yani teoremin şartları var, teorem şöyle:
a'yı içeren bir "I" açık aralığında (yani pozitif bir δ için (a-δ,a+δ) açık aralığında), f ve g fonksiyonları türevlenebilir ise yani bu aralıktaki tüm x'ler için f'(x) ve g'(x) varsa (yalnızca a hariç, yani x=a'da türevli olmak zorunda değiller, olabilirler de), ve bu aralıktaki tüm x'ler için g'(x)≠0 ise
(belki "a" hariç, yani g'(a)=0 olabilir), ve
lim x->a f(x)=0 ve lim x>a g(x)=0 ise, ve
lim x->a [f'(x)/g'(x)] limiti varsa, o zaman
lim x->a [f(x)/g(x)] = lim x->a [f'(x)/g'(x)]. Bu soruda f fonksiyonu hakkında hiçbir şey bilmiyoruz, bu şartları sağlayıp sağlamadığını da bilmiyoruz, yani fonksiyon hakkında hiçbir şey bilmezken L'hopital uygulayamayız, bu soruda L'hopital kullanamayız.
< Bu mesaj bu kişi tarafından değiştirildi miGma -- 29 Nisan 2021; 7:55:4 >
-
çok teşekkürler hocam benim hatam. pay ve paydanın limitini ayrı düşünmek aklıma gelmedi. direkt yerine yazmak hatalı oluyor
< Bu ileti Android uygulamasından atıldı >
Bu mesaj IP'si ile atılan mesajları ara Bu kullanıcının son IP'si ile atılan mesajları ara Bu mesaj IP'si ile kullanıcı ara Bu kullanıcının son IP'si ile kullanıcı ara
KAPAT X






 Yeni Kayıt
Yeni Kayıt







 Konudaki Resimler
Konudaki Resimler


 kullanıcısına yanıt
kullanıcısına yanıt
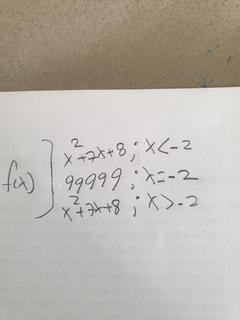


 Hızlı
Hızlı 



















